
SIS - Safety Instrumented Systems - A practical view - Part 2


César Cassiolato
Introduction
The Safety Instrumented Systems are used to monitor the condition of values and parameters of a plant within the operational limits and, when risk conditions occur, they must trigger alarms and place the plant in a safe condition or even at the shutdown condition.
The safety conditions should be always followed and adopted by plants and the best operating and installation practices are a duty of employers and employees. It is important to remember that the first concept regarding the safety law is to ensure that all systems are installed and operated in a safe way and the second one is that instruments and alarms involved with safety are operated with reliability and efficiency.
The Safety Instrumented Systems (SIS) are the systems responsible for the operating safety and ensuring the emergency stop within the limits considered as safe, whenever the operation exceeds such limits. The main objective is to avoid accidents inside and outside plants, such as fires, explosions, equipament damages, protection of production and property and, more than that, avoiding life risk or personal health damages and catastrophic impacts to community. It should be clear that no system is completely immune to failures and, even in case of failure; it should provide a safe condition.
For several years, the safety systems were designed according to the German standards (DIN V VDE 0801 and DIN V 19250), which were well accepted for years by the global safety community and which caused the efforts to create a global standard, IEC 61508, which now works as a basis for all operational safety regarding electric, electronic systems and programmable devices for any kind of industry. Such standard covers all safety systems with electronic nature.
Products certified according to IEC 61508 should basically cover 3 types of failures:
- Random hardware failures
- Systematic failures
- Common causes failures
IEC 61508 is divided in 7 parts, where the first 4 are mandatory and the other 3 act as guidelines:Part 1: General requirements
- Part 2: Requirements for E/E/PE safety-related systems
- Part 3: Software requirements
- Part 4: Definitions and abbreviations
- Part 5: Examples of methods for the determination of safety integrity levels
- Part 6: Guidelines on the application of IEC 61508-2 and IEC 61508-3
- Part 7: Overview of techniques and measures
Such standard systematically covers all activities of a SIS (Safety Instrumented System) life cycle and is focused on the performance required from a system, that is, once the desired SIL level (safety integrity level) is reached, the redundancy level and the test interval are at the discretion of who specified the system.
IEC61508 aims at potentializing the improvements of PES (Programmable Electronic Safety, where the PLCs, microprocessed systems, distributed control systems, sensors, and intelligent actuators, etc. are included) so as to standardize the concepts involved.
Recently, several standards on the SIS development, project and maintenance were prepared, as IEC 61508 (overall industries) already mentioned, and is also important to mention IEC 61511, focused on industries with ongoing, liquid, and gas process.
In practice, in several applications it has been seen the specification of equipment with SIL certification to be used in control systems, without safety function. It is also believed that there is a disinformation market, leading to the purchase of more expensive pieces of equipment developed for safety functions where, in practice, they will be used in process control functions, where the SIL certification does not bring the expected benefits, making difficult, inclusive, the use and operation of equipment.
In addition, such disinformation makes users to believe that they have a certified safe control system, but what they have is a controller with certified safety functions.
With the increase of usage and applications with digital equipment and instruments, it is extremely important that professionals involved on projects or daily instrumentation are qualified and have the knowledge on how to determine the performance required by the safety systems, who have domain on calculations tools and risk rates within the acceptable limits.
In addition, it is necessary to:
- Understand the common mode failures, know which types of safe and non-safe failures are possible in a specific system, how to prevent them and, also, when, how, where and which redundancy level is more appropriate for each case.
- Define the preventive maintenance level appropriate for each application.
The simple use of modern, sophisticated or even certified equipment does not absolutely ensure any improvement on reliability and safety of operation, when compared with traditional technologies, except when the system is deployed with criteria and knowledge of advantages and limitations inherent to each type of technology available. In addition, the entire SIS life cycle should be in mind.
Commonly we see accidents related to safety devices bypassed by operation or during maintenance. Certainly it is very difficult to avoid, in the project stage, that one of such devices are bypassed in the future, but by a solid project that better satisfies the operational needs of the safety system user, it is possible to considerably eliminate or reduce the number of non-authorized bypass.
By using and applying techniques with determined or programmable logic circuits, failure-tolerant and/or safe failure, microcomputers and software concepts, today is possible to project efficient and safe systems with costs suitable for such function.
The SIS complexity level depends a lot on the process considered. Heaters, reactors, cracking columns, boilers, and stoves are typical examples of equipment requiring safety interlock system carefully designed and implemented.
The appropriate operation of a SIS requires better performance and diagnosis conditions compared to the conventional systems. The safe operation in a SIS is composed by sensors, logic programmers, processors and final elements designed with the purpose of causing a stop whenever safe limits are exceeded (for example, process variables such as pressure and temperature over the very high alarm limits) or event preventing the operation under unfavorable conditions to the safe operation conditions.
Typical examples of safety systems:
- Emergency Shutdown System
- Safety Shutdown System
- Safety Interlock System
- Fire and Gas System
We have seen in the previous article, in the first part, some details on the Safety Life Cycle and Risk Analysis. Now we will see, in the second part, a little aboutReliability Engineering
Reliability of Measurement Systems
The reliability of the measurement systems may be quantified as the mean time between the failures occurring in the system. In this context, a failure means the occurrence of an unexpected condition that causes an incorrect value in the output.
Reliability Principles
The reliability of a measurement system is defined as the ability of a system executing its function within the operating limits and conditions during a defined time period. Unfortunately, several factors, such as manufacturer’s tolerance according to operating conditions sometimes make difficult such determination and, in practice, what we can get is statistically expressing the reliability by failure probabilities occurring within a time period.
In practice, we face a great difficulty, which is determining what is a failure. When the output of a system is incorrect, this is something hard to be interpreted compared with the overall loss of the measurement output.
Quantification of Reliability in almost absolute terms
As seen before, reliability essentially has a probability nature and can be quantified in almost absolute terms by mean time between failures (MTBF) and mean time to failure (MTTF). Importantly, those two times are usually the mean values calculated using an identical number of instruments and, therefore, for any particular instrument its values may be different from the average.
The MTBF is a parameter expressing the mean time between failures occurring in an instrument, calculated in a specific period of time. In cases where the equipment has high reliability, in practice, it will difficult to count the number o failures occurrences and non-precise number may be generated for the MTBF and, then, using the manufacturer value is recommended.
The MTTF is an alternative mode to quantify reliability. It is normally used for devices such as thermocouples, as they are discharged when they fail. MTTF expresses the mean time before the failure occurs, calculated in an identical number of devices.
The final associated reliability in terms of importance to the measurement system is expressed by the mean time to repair, that is, the mean time to repair an instrument or even the mean time to replace an equipment.
The combination of MTBF and MTTR shows the availability:
Availability = MTBF/ (MTBF+MTTR)
The availability measures the proportion of time in which the instrument works without failures.
The objective with measurement systems is to maximize the MTBF and minimize the MTTR and, consequently, maximize the Availability.
Failure Models
The failure mode in a device may change throughout its life cycle. It may remain unchanged, decrease or, at least, increase.
In electronic devices, it is common to have a behavior according to figure 1, also know as the bathtub curve.
Figure 1 - Typical Curve of reliability variation of an electronic component
Manufacturers usually apply burn-in tests in a way to eliminate the phase until T1, until products are placed in the market.
But the mechanical components will have a higher failure rate in the end of their life cycle, as per figure 2.
.jpg)
Figure 2 - Typical Curve of reliability variation of a mechanical component
In practice, where systems are electronic and mechanical compositions, the failure models are complex. The more components, the higher the incidents and probabilities of failures.
Reliability Laws
In the practice, usually we will have several components, and the measurement system is complex. We may have components in series or in parallel.
Reliability of components in series should take into consideration the probability of individual failures in a time period. For a measurement system with n components in series, reliability Rs is the product of individual reliabilities: Rs = R1xR2...Rn.
Imagine we have a measurement system composed by a sensor, a conversion element and a circuit of signal processing, where we have the following reliability: 0.9, 0.95 and 0.099, respectively. In such case, the system reliability will be:
0.9x0.95x0.009 = 0.85.
The reliability can be increased by placing components in parallel, what means that the system fails if all components fail. In such case, reliability Rs is demonstrated by:
Rs = 1 – Fs, where Fs is the non reliability of the system.
The non-reliability is Fs = F1xF2...F3.
For example, in a safe measurement system, there are three identical instruments in parallel. The reliability of each one is 0.95 and that of the system is:
Rs = 1 – [ (1-0.95)x(1-0.95)x(1-0.95)] = 0.999875
Improving the reliability of a measurement system
What we look for, in the practice, is to minimize the level of failures. An important requirement is to ensure one knows and act before T2 (see figures 1 and 2), when the statistical frequency of failures increases. The ideal is to make T (time period or life cycle) is equal to T2 and, then, maximizing the period without failures.
There are several ways to increase the reliability of a measurement system:
- Choice of instruments: One should always be aware to the instruments specified, its influences regarding the process, materials, environment, etc.
- Protection of instruments: protecting the instruments with appropriate protections may help to improve and ensure a higher level of reliability. For example, thermocouples should be protected in adverse operation conditions.
- Regular calibration: Most of the failures may be caused by drifts that may change and generate incorrect outputs. Therefore, according to the good instrumentation practices, we recommend that the instruments are periodically checked and calibrated.
- Redundancy: In such case, there is more than one equipment working in parallel and locked with a key, sometimes, automatically. Here the reliability is significantly improved.
Safety and Reliability Systems
The Safety Systems are used to monitor the condition of values and parameters of a plant within the operational limits and, when risk conditions occur, they must trigger alarms and place the plant in a safe condition or even at the shutdown condition.
Note that the safety conditions should be followed and adopted by plants where the best operating and installation practices are a duty of employers and employees. It is important to remember that the first concept regarding the safety law is to ensure that all systems are installed and operated in a safe way and the second one is that instruments and alarms involved with safety are operated with reliability and efficiency.
The Safety Instrumented Systems (SIS) are the systems responsible for the operating safety and ensuring the emergency stop within the limits considered as safe, whenever the operation exceeds such limits. The main objective is to avoid accidents inside and outside plants, such as fires, explosions, equipment damages, protection of production and property and, more than that, avoiding life risk or personal health damages and catastrophic impacts to community. It should be clear that no system is completely immune to failures and, even in case of failure; it should provide a safe condition.
Metrics used in the Reliability Engineering field involving SIS
1. Reliability R(t)
Reliability is a metric developed to determine the probability of success of an operation in a specified period of time.
.jpg)
When 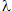 (failure rate) is too low, the non-reliability function (F(t)) or the Probability of Failure (PF) is shown by: PF(t) =
(failure rate) is too low, the non-reliability function (F(t)) or the Probability of Failure (PF) is shown by: PF(t) = 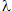 t
t
.jpg)
Figure 3 - Reliability R(t)
2. MTTR = Mean Time to Repair
The reliability measurement requires that a system has success in an operation during a time interval. In this sense, appears the MTTR metrics, which is the time in which is detected a failure and its repair occurs (or the reestablishment of operating success).
The reestablishment of the operating success is shown by: µ = 1/MTTR
In practice, it is not simple to estimate that rate, mainly when periodic inspection activities occur, as the failure may occur just after an inspection.
3. MTBF – Mean Time Between Failures
The MTBF is a basic measure of the reliability in repairable items of a piece of equipment. It may be expressed in hours or years. It is commonly used in systems reliability and sustainability analysis and can be calculated by the following formula:
MTBF = MTTR + MTTF
Where:
- MTTR = Mean Time to Repair
- MTTF = Mean Time to Failure = the inverse of the sum of all failures rates
As the MTTR is too low in practice, it is common to assume the MTBF = MTTF
4. Availability A(t) and Unavailability U(t)
Another very useful metric is the availability. It is defined as the probability of a device being available (without failures) when a time t requires it to operate within the operating conditions to which it was designed.
Unavailability is given by: U(t) = 1 – A(t)
Availability is not only a reliability function, but it is also a maintenance function. Table 1 below shows the relationship between reliability, maintenance and availability. Note in this table that an increase in the maintenance ability implies on a decrease in the time necessary to conduct the maintenance actions.
.jpg)
Table 1 - Relationship between Reliability, Maintenance and Availability
.jpg)
Figure 4 - Reliability, Availability and Costs
5. Probability of Failure on Demand (PFDavg) and Periodic Test and inspection
PFDavg is the probability of failure that a system (for failure prevention) has when a failure occurs. The SIL level is related to this probability of failure on demand and with the factor of risk reduction (how much needs to be protected to ensure an acceptable risk when a failure event occurs).
PFD is the Indicator of reliability appropriate for the safety systems.
If it is not tested, the failure probability tends to 1.0 with the time. Periodic tests maintain the probability of failure within the desired limit.
.jpg)
Figure 5 - Voting, PFD and Architecture
Figure 5 shows the architecture details versus the voting and PFD and figure 6 shows the correlation in PFD and Factor of Risk Reduction. Subsequently, we will discuss it in more details in the articles complementing this series.
.jpg)
Figure 6 - Correlation between PFDavg and Factor of Risk Reduction
The Failure Probability may be calculated using the following equation:
PFAvg = (Cpt x 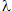 x TI/2) + ((1-Cpt) x
x TI/2) + ((1-Cpt) x 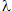 x L xT/2), where:
x L xT/2), where:
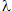 : failure rate:
: failure rate:- Cpt: percentage of failures detected by a test (proof test)
- TI: test period
- LT: life period of a process unit
Let’s see and example: Let’s suppose that a valve is used in a safety instrumented system and has an annual failure rate of 0.002. Every year a verification and inspection test is conducted. It is estimated that 70% of failures are detected in such tests. Such valve will be used for 25 years and its usage demand is estimated as once every 100 years. What is the average probability of failure?
Using the previous equation we have:
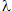 : 0.002
: 0.002- Cpt: 0.7
- TI: 1 year
- LT: 25 years
PFDavg = (0.7) x 0.002 x ½ + (1-0.7) x 0.002 x 25/2 = 0.0082
Conclusion
In practical terms, the aim is the reduction of failures and, consequently, the reduction of shutdowns and operational risks. The purpose is to increase the operational availability and also, in terms of processes, the minimization of variability with direct consequence to the profitability increase.
References
- IEC 61508 – Functional safety of electrical/electronic/programmable electronic safety-related systems.
- IEC 61511-1, clause 11, " Functional safety - Safety instrumented systems for the process industry sector - Part 1:Framework, definitions, system, hardware and software requirements", 2003-01
- ESTEVES, Marcello; RODRIGUEZ, João Aurélio V.; MACIEL, Marcos.Sistema de intertravamento de segurança, 2003.
- William M. Goble, Harry Cheddie, "Safety Instrumented Systems Verification: Practical Probabilistic Calculation"
- Safety Instrumented Systems - César Cassiolato
- “Reliability in Measurement Systems and Safety Instrumented Systems” - César Cassiolato
- Manual LD400-SIS
- Safety Instrumented Systems – a practical view – Parte 1, César Cassiolato
- Researches on internet







